Adding and Subtracting Square Roots
We’ve already covered the addition and subtraction of
numerical square roots in some detail. The procedure for adding
and subtracting square roots which may contain algebraic
expressions is more or less the same:
- simplify the square root in each term of the expression
- combine terms whose square roots are identical
We will illustrate this strategy with a number of simple
examples.
Example 1:
Simplify 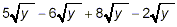
solution:
The square roots in all four of the terms in this expression
are identical, all being just 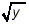 . So, we just collect
the “like terms": . So, we just collect
the “like terms":
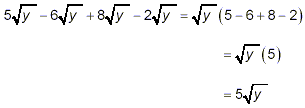
as the simplest form of the result.
Example 2:
Simplify 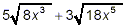
solution:
Neither of the two square roots occurring here are in simplest
form. So, to start, we must simplify each term.
Since
8x 3 = 2 3x 3 = 2 2
· 2 · x 2 · x
we can write
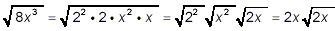
Also
18x 5 = 2 · 3 2 · (x 2)
2 x
and so
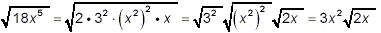
Thus
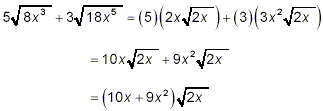
You could leave the final answer as this last expression, or
you could still do a bit of factoring to get, as the most
simplified form
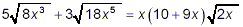
Example 3:
Simplify 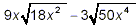
solution:
This example is very similar to Example 2 above, so you should
use it as a practice problem. Try to solve it yourself before
looking at our solution, given below.
First, simplify the individual square roots where possible.
Since
18x 2 = 2 · 3 2 · x 2
we get
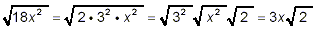
and since
50x 4 = 2 · 5 2 · (x 2) 2
we get
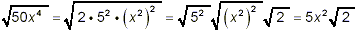
Thus
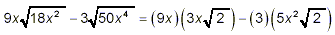
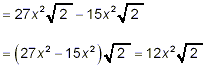
as the final answer.
Example 4:
Simplify 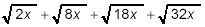
solution:
The last three of the square roots here can be simplified
slightly:
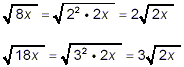
and
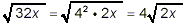
Thus,
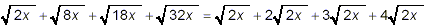
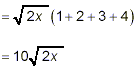
as the final result.
|