Adding Fractions

The objective of this lesson is very succinct:

• That you learn how to add fractions correctly

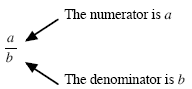
Numerator and Denominator

The number or algebraic expression that appears on the top line of a fraction is called the numerator of the fraction.

The number of algebraic expression that appears on the bottom line of a fraction is called the denominator of the fraction.

Adding Fractions

Expressed in symbols, the rule for adding fraction is as follows:

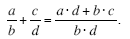
Let’s break this down to see everything that is expressed in this rule.

The numerator of the sum is a·d + b·c.

You can remember the numerator without having to memorize this particular formula by remembering the pattern of cross-multiplying. To create the numerator, you multiply each numerator by the opposing denominator, forming a “cross” pattern.

To get the denominator of the sum, you just multiply the two denominators (b and d) together.

Example

Work out each of the following sums of fractions.

Solution

(a)

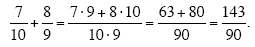
Often it will be possible for you to simplify your fractional expressions by combining “like terms” just as you do when FOILing a polynomial. Although this kind of simplification is not always needed just to get the right answer, if can make your fractional expressions much easier to deal with. Remember to keep the numerator and denominator separate when combining like terms!

(b)

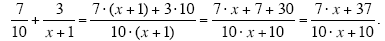
In Example (b), note how when the cross-multiplication is done, the “7” from the numerator of the first fraction multiplies the entire quantity (x + 1) that is in the denominator of the second fraction, not just the x. Also notice that when the two denominators are multiplied to create the denominator of the sum, the “10” from the denominator of the first fraction multiplies everything (i.e. the entire quantity (x + 1)) that appears in the denominator of the second fraction.

(c)

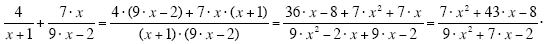
When simplifying fractions, simplify the numerator and denominator separately. You cannot combine like terms from the numerator with like terms from the denominator (or vice versa). Often you will need to FOIL when simplifying the numerator and denominator of fractions that involve algebraic expressions such as x.

(d)

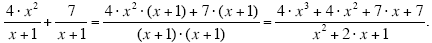
This answer is not the simplest one that is possible. If you look closely at the middle fraction above, you can see that every single term in the numerator has at least one factor of (x + 1). The denominator also has a factor of (x + 1). These “common” factors can be factored out of the numerator and the denominator as shown below.

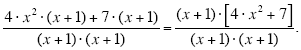
When you have a common factor that you have pulled out of every term in the numerator, and it matches a factor that shows up in the denominator, you can almost always cancel this factor from both the numerator and the denominator.

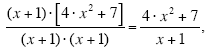provided x ≠ -1.

The only situation when it is not okay to cancel the factor of (x + 1) from the top and bottom is when you have the x-value of x = -1 (i.e. the particular x-value that makes the factor of (x + 1) equal to zero).