Polynomials
An expression such as 9p is a term; the number 9 is the
coefficient, p is the variable, and 4 is the exponent. The
expression p is a term; the number 9 is the
coefficient, p is the variable, and 4 is the exponent. The
expression p means p . p . p . p while p means p . p . p . p while p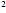 means p .
p and so on. Terms having the same variable and the same
exponent, such as 9x means p .
p and so on. Terms having the same variable and the same
exponent, such as 9x and -3x and -3x are like
terms. Terms that do not have both the same variable and the same
exponent, such as m are like
terms. Terms that do not have both the same variable and the same
exponent, such as m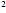 and m and m are
unlike terms. A polynomial is a term or a finite sum of terms in
which all variables have whole number exponents, and no variables
appear in denominators. Examples of polynomials include are
unlike terms. A polynomial is a term or a finite sum of terms in
which all variables have whole number exponents, and no variables
appear in denominators. Examples of polynomials include
5x + 2x
+ 2x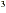 + 6x, 8m
+ 6x, 8m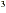 + 9m + 9m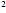 n - 6mn n - 6mn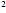 + 3n + 3n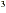 , 10 p,
and -9 , 10 p,
and -9
Adding and Subtracting Polynomials
The following properties of real numbers are useful for
performing operations on polynomials.
PROPERTIES OF REAL NUMBERS
For all real numbers a, b, and c,
1. Commutative properties:
a + b = b + a
ab = ba
2. Associative properties
(a + b) + c = a + (b + c)
(ab)c = a(bc)
3. Distributive property
a(b + c) = ab + ac
EXAMPLE 1
Properties of Real Numbers
(a) 2 + x = x + 2 Commutative property of addition
(b) x.3 = 3x Commutative property of multiplication
(c) (7x)x = 7(x.x) = 7x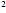 Associative property of multiplication Associative property of multiplication
(d) 3(x + 4) = 3x + 12 Distributive property
The distributive property is used to add or subtract
polynomials. Only like terms may be added or subtracted. For
example,
12y + 6y + 6y = (12 + 6)y = (12 + 6)y = 18y = 18y
and
-2m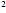 + 8m
+ 8m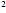 = (-2 + 8)m
= (-2 + 8)m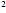 = 6m = 6m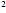
but the polynomial 8y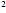 + 2y + 2y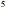 cannot be further simplified. To subtract
polynomials, use the facts that -(a+b)=-a-b and -(a-b)=-a+b In
the next example, we show how to add and subtract polynomials. cannot be further simplified. To subtract
polynomials, use the facts that -(a+b)=-a-b and -(a-b)=-a+b In
the next example, we show how to add and subtract polynomials.
|