Solving Quadratic Equations Graphically and Algebraically
A quadratic equation is an equation that can be simplified to follow the pattern:
y = a · x2 + b· x + c,
where the letter x represents the input, the letter y represents the value of the output and
the letters a, b and c are all numbers. Sometimes the numbers a, b and c are referred to as
coefficients.
Solving a Quadratic Equation
Just as you did for linear and power equations, you solve a quadratic equation when you
have been given a y-value and need to find all of the corresponding x-values. For
example, if you had been given the quadratic equation:
y = x2 + 8 · x +10,
and the y-value,
y = 30,
then solving the quadratic equation would mean finding all of the numerical values of x
that work when you plug them into the equation:
x2 + 8 · x +10 = 30.
Note that solving this quadratic equation is the same as solving the quadratic equation:
x2 + 8 · x +10 - 30 = 30 - 30 (Subtract 30 from each side)
x2 + 8 · x - 20 = 0 (Simplify)
Solving the quadratic equation
x2 + 8 · x - 20 = 0 will give exactly the same values for x
that solving the original quadratic equation,
x2 + 8 · x +10 = 30, will give.
The advantage of manipulating the quadratic equation to reduce one side of the equation
to zero before attempting to find any values of x is that this manipulation creates a new
quadratic equation that can be solved using some fairly standard techniques and formulas.
Solving a Quadratic Function Graphically Using a Graphing Calculator
When you are trying to solve a quadratic equation of the form:
a · x2 + b · x + c = 0,
the solutions are the x-coordinates of the points where the graph of the quadratic equation
y = a· x2 + b· x + c cuts the horizontal axis.
From a graphical point of view, the solutions of the manipulated quadratic formula:
x2 + 8 · x - 20 = 0,
are the x-values where the graph of
y = x2 + 8 · x - 20 cuts the horizontal x-axis. (These
points, x = 2 and x = -10, are shown in Figure 1).
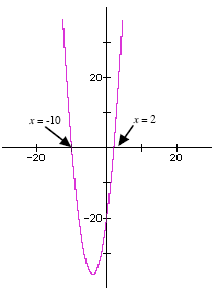
Figure 1: Graphical representation of the
solutions of a quadratic equation.
There may be zero, one or two places where
the graph of the quadratic equation
y = a · x2 + b· x + c cuts the horizontal x-axis
(see Figure 2, below). This means that the
quadratic equation:
a · x2 + b · x + c = 0,
can have zero, one or two solutions.
You can determine the number of solutions
that a quadratic equations has by calculating
the discriminant,Δ. The discriminant is equal
to:
Δ = b2 - 4 · a · c .
The sign of the discriminant tells you the
number of solutions that exist for the
quadratic equation,
a · x2 + b · x + c = 0.
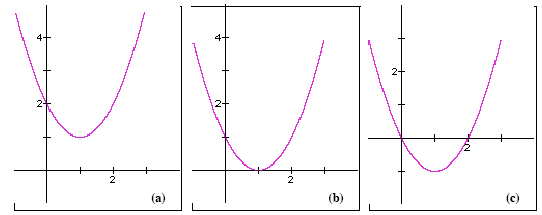
Figure 2: (a) A quadratic equation with zero solutions. (b) A quadratic equation with exactly one solution. (c) A quadratic
equation with exactly two solutions.
| Sign of discriminant, Δ = b2 - 4
· a · c |
Number of solutions of quadratic equation,
a · x2 + b · x + c = 0 |
| Negative (-) |
Zero solutions |
| Zero (0) |
Exactly one solution |
| Positive (+) |
Exactly two solutions.
|
Table 1: Determining the number of solutions using the sign of the discriminant.
|