The Quadratic Formula
Here we apply the method for completing the square to the general quadratic equation to get a formula
for the solutions to any quadratic equation.
Developing the Formula
Start with the general form of the quadratic equation,
ax2 + bx + c = 0.
Assume a is positive for now, and divide each side by a:
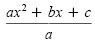 |
 |
|
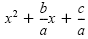 |
= 0 |
Subtract
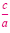 from each side. from each side. |
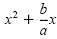 |
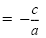 |
|
One-half of
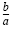 is is
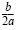 , and , and
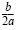 squared is squared is
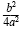 : :
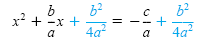
Factor the left-hand side and get a common denominator for the right-hand side:
We assumed a was positive so that
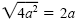 would be correct. If a is negative,
then would be correct. If a is negative,
then
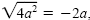 , and we get , and we get
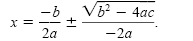
However, the negative sign can be omitted in -2a because of the
± symbol preceding
it. For example, the results of 5 ± (-3) and 5
± 3 are the same. So when a
is negative, we get the same formula as when a is positive. It is called the quadratic formula.
The Quadratic Formula
The solution to ax2 + bx + c = 0, with a
≠ 0, is given by the formula
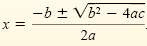
|