Polynomials
- A term is a number, a variable, or a
product of numbers and variables.
- A monomial is a term in which the
variables are only raised to whole number powers.
- A polynomial is a monomial or sum of
monomials.
- A monomial is a polynomial with only one
term.
- A binomial is a polynomial with exactly
two terms.
- A trinomial is a polynomial with exactly
three terms.
- Polynomials don’t, in the usual sense, have size (in
the way that numbers do, that is). Sometimes, however,
it’s necessary to compare the relative
“sizes” of two polynomials anyway. To do that,
we use the concept of degree.
- The degree of a term with just one
variable is the power to which the variable gets raised.
(This is 0 if there is no variable.)
- The degree of a polynomial is the
largest degree of any of its terms.
- It is common two write polynomials in decending powers of
the variable, or descending order. This
leads to two more pieces of vocabulary.
- The leading term of a polynomial is the
term with the highest degree.
- The leading coefficient is the
coefficient of the leading term.
- Simplifying a polynomial requires that you combine all
like terms.
- For polynomials with only one variable, “like
terms” means that the power of the variable
is the same. For example, 3x 5 and -2x 5
are like terms, but 2a 4 and 2a 2
are NOT.
- You CANNOT combine terms that are not
“like”. For example, there is no way to add x
3 and x 2. ( x 3 + x 2
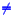 x 5 = x 2 x 3
). x 5 = x 2 x 3
).
- Keep in mind that the variable in a polynomial represents
a number. Every time a variable appears, it represents
the SAME number. For example, if x = 2, then the
polynomial x 3 - 5x 2 + x - 5 is
the same as 2 3 - 5(2 2) + 2 - 5 =
8 - 20 + 2 - 5 = -15.
|