Simplifying Square Roots
An expression containing a square root is considered to be as
simple as possible when the expression inside the square root is
as simple or small as possible. The reduction of the contents
inside the square root is accomplished (when possible) by a very
straightforward strategy:
(i) Factor the expression inside the square root completely.
Write factors which are perfect squares as explicit squares.
(ii) Use the property that the square root of a product is
equal to the product of the square roots of the factors to
rewrite the square root from step (i) as a product of square
roots of factors which are perfect squares and a single square
root of an expression which contains no perfect square factors.
The pattern is:
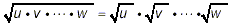
where u, v, etc. are perfect squares, and w is an expression
containing no perfect square factors. (This may seem a bit
abstract, but the meaning of this pattern should become more
obvious after you have studied a few of the examples below. It is
important in mathematics not only to study specific examples of a
type of operation, but to eventually understand an overall
general strategy or pattern for similar types of problems.
(iii) Replace the square roots of perfect squares by factors
which are not square roots using the property
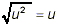
We now illustrate this general strategy with a series of
specific examples.
Example 1:
Simplify 
solution:
The expression inside the square root is nearly completely
factored already, but we do need to write it so that perfect
square factors show up more explicitly to complete step (i) in
applying the general strategy given above. We have
50 = 2 · 5 · 5 = 2 · 5 2 and x 13 = x
12 · x = (x 6) 2 · x
Thus our original square root can be rewritten as
 |
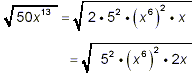after rearranging the order of the
factors. Now we can do step (ii) of the strategy:
separate the perfect square factors in this square root
into individual square root factors. |
 |
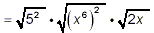now we can apply step (iii) of the
strategy to the first two factors … |
 |
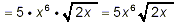to get our final result. |
Notice that the remaining square root factor in this final
expression, 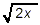 , contains no further
perfect square factors, and so there is no way to reduce the
expression inside this remaining square root any further. Thus,
our final answer is:
Even though you can probably do the first step of this
strategy – the factorization to show perfect square factors
– without writing down a lot of intermediate steps, we
suggest that you do write down enough of the details to reliably
keep track of what you are doing. It is particularly important to
ensure that the perfect squares that you identify are accurate,
and the best way to do that is to show at least as much work as
we did in the solution to Example 1 above. For powers of symbols,
even powers are always perfect squares. Odd powers are a product
of a perfect square and the first power of that symbol.
Example 2:
Simplify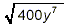 
solution:
First, we factor the expression inside the square root to
display all possible perfect square factors explicitly. Methods
for ensuring a complete factorization of numbers into a product
of prime factors have been covered elsewhere in these notes.
400 = 2 · 200 = 2 · 2 · 100 = 2 · 2 · 2 · 50 = 2 · 2 ·
2 · 2 · 25 = 2 · 2 · 2 · 2 · 5 · 5 = 2 4 · 5
2 = (2 2 ) 2 · 5 2
and
y 7 = y 6 · y = (y 3 )
2 y
So,
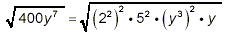
as the final answer.
Example 3:
Simplify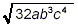 
solution:
Here
32 = 2 5 = (2 2 ) 2 · 2
and
ab 3c 4 = a · b 2 · b · (c
2) 2 = b 2(c 2) 2
· ab
So
|
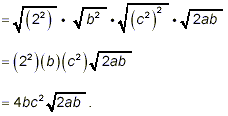
