The Pythagorean Theorem
The Pythagorean Theorem states that in a
right triangle, the square of the length of the hypotenuse is
equal to the sum of the squares of the lengths of the legs.
The famous formula that resumes this phrase is c 2
= a 2 + b 2
Example 1
The measurements of three sides of a triangle are 5, 6, and 7
units. Determine whether the triangle is a right triangle.
Solution
Use the Pythagorean Theorem to see if the square of the length
of the hypotenuse is equal to the sum of the squares of the
lengths of the legs.
| c 2 |
= a 2 + b 2 |
|
| 7 2 |
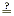 5 2 + 6 2 5 2 + 6 2 |
The hypotenuse is the longest side. |
| 49 |
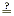 25 + 36 25 + 36 |
|
| 49 |
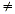 61 61 |
|
Since 7 2 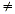 5 2 + 6 2 , the triangle is not a right
triangle.
5 2 + 6 2 , the triangle is not a right
triangle.
Sometimes, when working with the Pythagorean Theorem, one has
to approximate square roots. Consider the following example.
Example 2
Find the length of the third side of the right triangle.
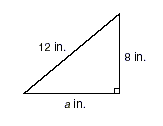
Solution To find the length of the third
side, use the Pythagorean Theorem.
| c 2 |
= a 2 + b 2 |
Pythagorean Theorem |
| 12 2 |
= a 2 + 8 2 |
Replace c with 12 and b with 8. |
| 144 |
= a 2 + 64 |
|
| 144 - 64 |
= a 2 |
Subtract 64 from each side. |
| 80 |
= a 2 |
|
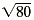 |
= a |
Take the square root of each side. |
| 8.9 |
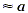 |
|
The length of the leg is about 8.9 inches.
Try to find several problems involving the Pythagorean Theorem
as it addresses geometric and algebraic concepts, and practices
skills such as taking square roots.
|