Solving Quadratic Equations
Strategies for Solving Quadratic Equations
You have learned four ways to solve a quadratic equation:
• The Square Root Property
• Factoring
• Completing the square
• The quadratic formula
You can solve any quadratic equation by completing the square or by
using the quadratic formula. However, for some quadratic equations, it is
quicker to solve by factoring or by using the Square Root Property.
When you want to solve a quadratic equation, try the following strategies:
1. Use the Square Root Property when the equation can be easily
written in the form x2 = a or (x + k)2 = a.
| For example, the Square Root Property
is useful for solving this equation:
Add 16 to both sides. |
(x + 3)2 - 16 = 0
(x + 3)2 = 16 |
| Use the Square Root Property
to write two linear equations.
|
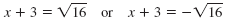 |
| Simplify each square root.
Subtract 3 from both sides of
each equation. |
x + 3 = 4 or x + 3 = -4
x =1 or x = -7 |
2. If the Square Root Property cannot be easily applied, write the
equation in standard form, ax2 + bx + c = 0.
If the trinomial can be easily factored, solve the equation by
factoring.
| For example, this strategy is
useful for solving this equation:
Add 6 to both sides of the equation.
Factor the trinomial.
Set each factor equal to 0.
Solve each equation. |
x2 - 5x = -6
x2 - 5x + 6 = 0
(x - 2)(x - 3) = 0
x - 2 = 0 or x - 3 = 0
x = 2 or x = 3 |
3. The quadratic formula can be used to solve any quadratic equation,
including the equations in the two previous examples.
|