Solving Multi-Step Inequalities
Objective Learn to solve linear inequalities
involving more than one operation.
This lesson is an extension of the methods you should already
know to solve linear equations. The methods used are the Addition
and Multiplication Properties of Inequalities, which parallel the
corresponding properties for equalities. There are two
significant distinctions that must be remembered.
The first is that when multiplying or dividing an inequality
by a negative number, the direction of the inequality symbol must
be changed.
The other is that the term “solve” is used a bit
differently when speaking of inequalities. In equations,
“solve” means to find a particular number that is the
only solution to the equation. However, the result of solving an
inequality is never a single number but rather the description of
a set, such as x 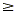 5 or 22 5 or 22 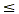 x x 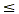 7. 7.
This distinction is very important.
Solving Inequalities
Let's begin by reviewing the properties of inequalities.
Addition and Subtraction Properties of Inequalities
Adding or subtracting a fixed number to each side of an
inequality produces an equivalent inequality. Any solution of
either inequality is a solution of the other.
| x - 2 |
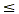 1 1 |
|
| x - 2 + 2 |
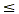 1 + 2 1 + 2 |
Add 2 to each side. |
| x |
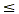 23 23 |
|
Adding 2 to each side of the original inequality shows that x
- 2 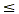 1 is equivalent to x 1 is equivalent to x 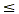 3. 3.
Multiplication and Division Properties of Inequalities
• Multiplying or dividing each side of an inequality by
the same positive number produces an equivalent inequality.
• Multiplying or dividing by the same negative number
produces an equivalent inequality if the direction of the
inequality symbol is reversed.
3x 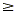 12 12 |
|
-x 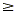 5 5 |
|
x 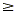 4 4 |
Divide each side by 3. |
x 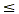 -5 -5 |
Multiply each side by -1. |
So, 3x 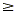 12 12 |
is equivalent to x 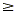 4. 4. |
So, -x 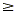 5 5 |
is equivalent to x 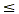 -5. -5. |
|