Completing the Square
Procedure —
To Complete the Square
To complete the square for a binomial of the form x2 + bx:
Step 1 Calculate
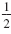 · b.
· b.
(That is, divide b by 2.)
Step 2 Square the result from Step 1.
That is, calculate
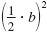 .
.
Step 3 Add the result from Step 2 to x2 + bx.
The new expression, x2 + bx +
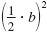 , is a perfect square
trinomial.
, is a perfect square
trinomial.
Example
Complete the square for each binomial. Then write each new expression as
the square of a binomial.
a. x2 + 12x
b. x2 - 5x
Solution
| a. |
x2 + 12x has the form x2
+ bx, where b = 12.
Step 1 Calculate
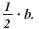
Step 2 Square the result from Step 1.
Step 3 Add the result from Step 2 to x2 + bx. |
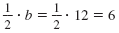
62 = 36
x2 + 12x + 36 |
| b. |
Write the expression x2 + 12x + 36 as the
square of a binomial. x2 - 5x has the form x2 + bx, where b
= -5. |
= (x + 6)2 |
| |
Step 1 Calculate
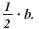
Step 2 Square the result from Step 1.
Step 3 Add the result from Step 2 to
x2 + bx. |

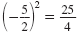
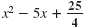 |
We have completed the square.
Write the expression as the square of a binomial.
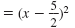
Notes:
The expression x2 + 12x + 36 is a perfect
square trinomial.
The expression
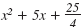 is a perfect
square trinomial. is a perfect
square trinomial.
|