Use of Parentheses or Brackets (The Distributive Law)
The Basic Idea
Pairs of parentheses or brackets
(such as ( ), [ ], { }, etc) are one way that is used to group
parts of an expression together to show exactly in what order the
arithmetic is to be done. Thus, for example, when we write
2(3 + 5)
we mean “add 3 to 5 first, then multiply the result by
2.” Thus
2(3 + 5) = 2 x 8 = 16 (*)
This expression can also be interpreted to mean that the
multiplication by 2 is to be done to every term inside the
brackets. Thus
2(3 + 5) = 2 x 3 + 2 x 5 = 6 + 10 = 16 (**)
which is the same final result as before. In the sequence of
steps in (**), we say that we are expanding the brackets. If we
use the symbols a, b, and c to represent any three numbers, then
the overall process in (**) can be symbolized as
a(b + c) = a × b + a ×c
The rule in the box above is called the distributive
law for multiplication. It shows how multiplication of
the bracketed expression by ‘a’ is
“distributed” to all of the terms in the brackets.
Be careful if there are minus signs inside the brackets. For
example
2(3 – 5) = 2(-2) = -4
and
2(3 – 5) = 2 x 3 + 2 x (-5) = 6 + (-10) = 6 – 10 =
-4
Thus, the minus sign must be retained when the brackets are
removed. In general
a(b - c) = a × b - a × c
An Illustration
You can visualize the equivalence between
2(3 + 5) and 2 × 3 + 2 × 5
by considering the following diagrams. We draw 16 dots
arranged in two rows as follows:
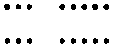
Each row has a group of three dots and a group of 5 dots, so
the number of dots in each of the two rows is 3 + 5 = 8 dots. Now
we can count the total number of dots in the diagram using the
following scheme:

That is, to get the total of 16 dots in the diagram, we count
8 dots in each of two rows, for a total of 16 dots:
2(3 + 5) = 2 × 8 = 16.
Alternatively, we could imagine grouping the dots in a
different way for counting:

This last diagram counts the dots according the process
2 × 3 + 2 × 5 = 6 + 10 = 16.
By comparing the last two diagrams, you can see how the
equivalence between the two expressions
2(3 + 5) and 2 × 3 + 2 × 5
comes about. In this illustration, the two expressions just
amount to counting the same array of 16 dots, but tallying the
dots in different orders.
|