Solutions to Linear Equations in Two Variables
In this section
we will learn to use that same technique to determine if given values as points (x, y) make a
true
statements of linear equations in two variables. These points are called solutions or
truth values.
We will also build tables as sequences of truth values.
EXAMPLES:
1. Given 2x − 3y = 6 use the replacement values for the points (x, y) to see if the points lie on the
line defined by the equation. [That is, see if the points make a true statement of the equation.]
Do the points (3, 0), (-3, -3) , (0, -2), (6, 2) satisfy the equation?
Use the points as replacements:
| 2(3) − 3(0) = 6 ?? |
6 − 0 = 6
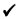 |
This point is on the line. |
| 2(-3) − 3(-3) = 6 ?? |
-6 − (-9) ≠ 6
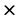 |
This point is not on the line. |
| 2(0) − 3(-2) = 6 ?? |
0 − (-6) = 6
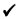 |
This point is on the line. |
| 2(6) − 3(2) = 6 ?? |
12 − 6 = 6
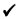 |
This point is on the line. |
2. Given 5x + 2y = 10 use the replacement values for the points (x, y) to see if the points lie on
the line defined by the equation. [That is, see if the points make a true statement of the
equation.]
Do the points (2, 0), (-2, 10), (4, -2) (0, 5) satisfy the equation?
Use the points as replacements:
| 5(2) + 2(0) = 10 ?? |
10 + 0 = 10
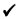 |
This point is on the line. |
| 5(-2) + 2(10) = 10 ?? |
-10 + 20 = 10
 |
This point is on the line. |
| 5(4) + 2(-2) = 10 ?? |
20 + (- 4) ≠ 10
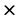
|
This point is not on the line. |
| 5(0) + 2(5) = 10 ?? |
0 + 10 = 10
|
This point is on the line. |
NOTE: This method can be used to check your points and solutions to applications.
|