Solving Rational Inequalities with a Sign Graph
Example
Solving a rational inequality
Solve
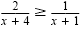 and graph the solution set.
Solution
We do not multiply by the LCD as we do in solving equations. Instead, subtract
 from each side:
 |
≥ 0 |
|
 |
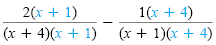≥ 0 |
Get a common denominator. |
 |
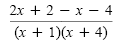≥ 0 |
Simplify. |
 |
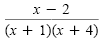≥ 0 |
|
Make a sign graph as shown in the figure below.
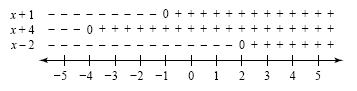
The computation of
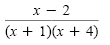
involves multiplication and division. The result of this computation is positive if all
of the three binomials are positive or if only one is positive and the other two are
negative. The sign graph shows that this rational expression will have a positive
value when x is between -4 and -1 and again when x is larger than 2. The solution
set is (-4, -1) È [2, ∞). Note that
-1 and -4 are not in the solution set because
they make the denominator zero. The graph of the solution set is shown in
the figure below.
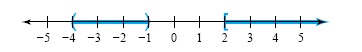
Solving rational inequalities with a sign graph is summarized below.
Strategy for Solving a Rational Inequality
with a Sign Graph
1. Rewrite the inequality with 0 on the right-hand side.
2. Use only addition and subtraction to get an equivalent inequality.
3. Factor the numerator and denominator if possible.
4. Make a sign graph showing where each factor is positive, negative, or zero.
5. Use the rules for multiplying and dividing signed numbers to determine the
regions that satisfy the original inequality.
|
