Quadratic Expressions
Completing the Square
The starting position for each of the above cases was the
correct choice of the complete square. For example, part (a)
began with the expansion of ( x + 3)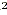 as x as x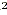 + 6 x + 9 and this information was used to
complete the square on x + 6 x + 9 and this information was used to
complete the square on x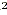 +6 x+10. In practice the starting point is
usually the quadratic expression, i.e., in (a) it would be x +6 x+10. In practice the starting point is
usually the quadratic expression, i.e., in (a) it would be x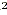 + 6 x + 10. The problem is to work directly
from this. The general procedure uses the following observation: + 6 x + 10. The problem is to work directly
from this. The general procedure uses the following observation:
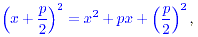
so the expression x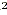 + px can be made into a complete square by
adding ( p/2) + px can be made into a complete square by
adding ( p/2)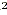 , i.e., by adding the square of half the
coeffcient of x. So as not to alter the expression the same
amount must be subtracted. In other words we use the equality , i.e., by adding the square of half the
coeffcient of x. So as not to alter the expression the same
amount must be subtracted. In other words we use the equality
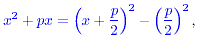
and this is the essence of completing the square.
Example 1
Complete the square on the following expressions.
(a) x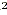 + 8 x + 15 , (b) x + 8 x + 15 , (b) x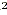 - 5 x + 6 . - 5 x + 6 .
Solution
(a) Completing the square means adding the square of half the
coefficient of x and then subtracting the same amount. Thus
x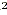 + 8 x + 15 = [ x + 8 x + 15 = [ x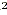 + 8 x] + 15 , + 8 x] + 15 ,
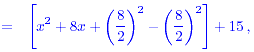
= [( x + 4)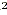 - 4 - 4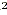 ] + 15 , ] + 15 ,
= ( x + 4)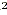 - 16 + 15 , - 16 + 15 ,
= ( x + 4)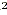 - 1 . - 1 .
(b) For x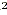 - 5x + 6 the procedure is much the same. - 5x + 6 the procedure is much the same.
x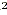 - 5x + 6 = [x - 5x + 6 = [x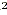 - 5x] + 6 , - 5x] + 6 ,
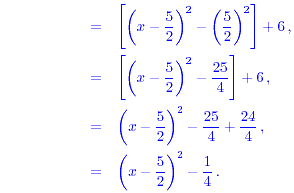
|