Quadratic Expressions

In the package on Factorizing Expressions we looked at how to factorize quadratic expressions which have the number 1 in front of the highest order term, x, y, z, etc.. If the highest order term has a number other than this then more work must be done to factorize the expression. As in the earlier case, some insight is gained by looking at a general expression with factors (ax + c) and (bx + d). Then

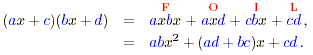
showing that the coeffcient of the square term, x, is ab, the product of the coeffcients of the x-terms in each factor. The coeffcient of the x-term is made up from the coeffcients as follows:

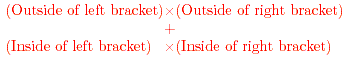
This is the information needed to find the factors of quadratic expressions.

Example 1

Factorize the following expressions.

(a) 2x + 7x + 3 , (b) 10x + 9x + 2 .

Solution

(a) The factors of 2 are 2 and 1, and the factors of 3 are 3 and 1. If the quadratic expression factorizes then it is likely to be of the form (2x + c)(1x + d) and the choice for c, d is 3, 1 or 1, 3. Trying the first combination,

(2x + 3)(x + 1) = 2x + 2x + 3x + 3 ,

= 2x + 5x + 3 (which is incorrect) .

The second choice is

(2x + 1)(x + 3) = 2x+ 6x + x + 3 ,

= 2x+ 7x + 3 , which is therefore the correct factorization.

(b) There is more than one choice for the first term since 10 is 1 × 10 as well as 2 × 5. The final term will factor as 2 × 1. Which combination of pairs, either (1, 10) with (2, 1), or (2, 5) with (2, 1), will give the correct coeffcient of x, i.e., 9? The latter two pairs seem the more likely since 2 × 2 + 5 × 1 = 9. Checking

(2x + 1)(5x + 2) = 10x + 4x + 5x + 2 ,

= 10x + 9x + 2 .

Exercise 1.

Factorize each of the following expressions.

(a) 2x + 5x + 3

(b) 3x + 7x + 2

(c) 3y - 5y - 2

(d) 4z - 23z + 15

(e) 64z + 4z - 3

(f) 4w - 25

Solution

(a) In this case we have 2x + 5x + 3 = (2x + 3)(x + 1)

(b) In this case we have 3x + 7x + 2 = (3x + 1)(x + 2)

(c) In this case we have 3y - 5y - 2 = (3y + 1)(y - 2)

(d) In this case we have 4z - 23z + 15 = (4z - 3)(z - 5)

(e) In this case we have 64z + 4z - 3 = (16z - 3)(4z + 1)

(f) This is a case of the difference of two squares which was seen in the package on Brackets. 4w - 25 = (2w - 5)(2w + 5)

Quiz

To which of the following does 12x2 + 17x - 14 factorize?

(a) (12x + 7)(x - 2) (b) (x + 2)(12x - 7) (c) (4x + 7)(x - 3) (d) (x - 7)(4x + 3)

Solution

There are several possibilities since the final term is -14 and the two quantities corresponding to c and d must therefore have opposite signs. The possible factors of 12 are (1, 12), (2, 6), (3, 4). For -14, the possible factors are (±1,14), (±2,7). It is now a matter of trial and error. The possible combinations are

(1, 12) and (±1,14) , (1, 12) and (±2,7) ,

(2, 6) and (±1,14) , (2, 6) and (±2,7) ,

(3, 4) and (±1,14) , (3, 4) and (±2,7) .

By inspection (2 × 12) + (1 × {-7}) = 24 - 7 = 17, so the factors appear to be (x + 2) and (12x - 7). This can easily be checked.

(x + 2)(12x - 7) = 12x - 7x + 24x - 14 ,

= 12x+ 17x - 14 ,

and the required factorization has been achieved.