Functions and Graphs
Definition of a Function
We often work with two quantities that are related.
For example, let’s say you put gas in your car. The total cost of the gas is
related to the number of gallons of gas you buy.
Suppose gas costs $1.50 per gallon. Then, the relationship between the
cost in dollars, y, and the number of gallons, x, is given by:
y = 1.50x
The equation y = 1.50x is an example of a function.
Definition —
Function
A function is a rule that assigns to each number in one set exactly
one number in another set.
The function y = 1.50x is a rule that says to start with a number,
represented by x, and to multiply that number by 1.50. The result is the
number represented by y. The ordered pair, (x, y) is said to satisfy the
function.
For example, the ordered pair (2, 3) satisfies the function y = 1.50x. This
is because replacing x with 2 and y with 3 results in a true statement:
Is 3 = 1.50 · 2 ?
Is 3 = 3 ? Yes
Example 1
In the function y = 1.50x, the variable y represents the cost in dollars and x
represents the number of gallons of gas purchased. Find the cost of
6 gallons of gas.
Solution
In the function, y = 1.50x, substitute 6 for x and simplify.
| Let x = 6 Multiply |
y = 1.50 (6) y = 9.00 |
So, the cost of 6 gallons of gas is $9.00.
The ordered pair (6, 9) satisfies the function y = 1.50x.
The two sets related by a function have special names. The first set is
called the domain of the function. A number in this set is called an input.
The input is usually represented by the letter x.The second set is called the
range of the function. A number in this set is
called an output. The output is often represented by the letter y.
Note:
You can think of a function as a machine
that assigns to each input number, x,
exactly one output number, y.

Here are three more examples of functions:
| Absolute Value
function |
Quadratic
function |
Square Root
function |
| y = - x2 - 6 |
y = 4|x| - 8 |
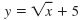 |
Function Notation
Functions can also be written in function notation, a special notation that
uses letters such as f, g, and h.
For example, when x is the input, the output may be written as f(x). This is
read, “f of xâ€. This notation shows that each output value is related to each
input value by the function, f.
For example,
y = - x2 - 6 is equivalent to f(x) = - x2 - 6
y = 4|x| - 8 is equivalent to g(x) = 4|x|
- 8
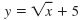 is equivalent to is equivalent to
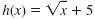
If we are given a value for x, we can find the corresponding value of the
function, f(x).Note:
In the past, you have used parentheses to
indicate multiplication. Thus, f(x) could
also be interpreted as the variable f
multiplied by the variable x.
The only way to tell if f(x) means function
or multiplication is to look at the context in
which it is used.
|