Multiplying and Dividing by Monomials
Multiplying Monomials
An expression like 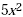 is called a monomial . A monomial is a number, a
variable, or a product of a number and one or more variables.
Monomials that are real numbers are called constants. To simplify
a product involving monomials, write an equivalent expression in
which: (1) there are no powers of powers, (2) each base appears
exactly once, and (3) all fractions are in simplest form.
| Product of Powers |
You can multiply powers with the same
base by adding exponents. For any number a, and all
integers m and n,  . |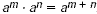
| Power of a Power |
You can find a power of a power by
multiplying exponents. For any number a, and all integers
m and n,  |
| Power of a Product |
A power of a product is the product of
the powers. For all numbers a and b, and any integer m,  |
| Power of a Monomial |
The power of a power property and the power of a
product property can be combined into the power of a
monomial property. For all numbers a and b, and all
integers m, n, and p  |
Dividing by Monomials
| Quotient of Powers |
You can divide powers with the same base
by subtracting exponents. For all integers m and n and
any nonzero number a,  |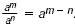
| Zero Exponent |
For any nonzero number a,  . |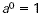
| Negative Exponents |
For any nonzero number a and any integer
n,  |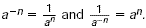
|
