Imaginary Numbers
You have seen that some quadratic equations have no real number
solutions.
| For example, let’s solve this quadratic equation:
First, we write the equation in the form x2 = a.
Next, we use the Square Root Property x
to write two equations: |
x2 + 1
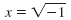 |
= 0 = -1
or |
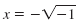 |
The solutions,
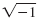 and and
 , are not real numbers because there is no
real number whose square is -1. , are not real numbers because there is no
real number whose square is -1.
In order to solve an equation such as x2 + 1 = 0, mathematicians defined
a new number, which they represented with the letter i.
Definition - i
The number i is defined as follows:
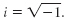
That is,
i2 = -1.
The number i is not a real number. Instead, i is an example of an
imaginary number.
Given the definition of i, we can write the solutions of x2 + 1 = 0 as follows:
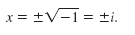
We check the solutions by replacing x with i or with -i in the original
equation:
| |
Check x = i |
|
Check x = -i |
| Is
Is
Is |
x2 + 1
(i)2 + 1
-1 + 1
0 |
= 0 ? = 0 ?
= 0 ?
= 0 ? Yes |
Is
Is
Is
Is |
x2 + 1
(-i)2 + 1
i2 + 1
-1 + 1
0 |
= 0 ? = 0 ?
= 0 ?
= 0 ?
= 0 ? Yes |
We can use an imaginary number to rewrite the square root of a negative
number.
Definition — Square Root of a Negative Number
If k is a positive real number, then
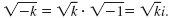
We can also write the i in front of the radical, like this:

Examples:
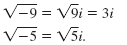
Note:
In an expression such as
 be sure to
write the i outside the radical symbol. be sure to
write the i outside the radical symbol.
Example
Simplify:
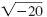
| Solution |
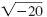 |
Rewrite
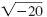 using using
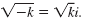 |
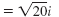 |
Simplify
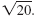 |
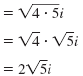 |
So,
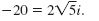
|