Multiplying Monomials
After studying this lesson, you will be able to:
- Multiply monomials.
- Multiply powers with the same base.
- Raise a power to a power.
Monomials have one term. The term can be a
number, a variable, or the product of a number and a variable.
Monomials are expressions with do not contain a + or - sign....
it has only one term.
Examples of monomials: 4, 4x, 4x 2,
-3x 2y, xyz
We will learn several exponent rules. It is very important
that you learn these immediately.
In the example 5 2, 5 is the Base
and 2 is the Power or Exponent
Multiplying Powers with the Same Base:
The base stays the same; Add exponents
Example 1
8 4 · 8 3
We are multiplying powers with the same base (8). So, we keep
the base and we add the exponents.
The answer will be 8 7
Example 2
y · y 2 · y 5
We are multiplying powers with the same base (y). So, we keep
the base and we add the exponents.
The answer will be y 8
Example 3
x 2 · x 4 · x
We are multiplying powers with the same base (x). So, we keep
the base and we add the exponents.
The answer will be x 7
Example 4
( x 2 y 3 )( x y 2
)
We are multiplying powers with the same base. Actually, we
have two bases (x and y). So, we keep the bases and we add the
exponents. We add the exponents of x (2 and 1) and we add the
exponents of y (3 and 2) to get the x 3 y 5
Example 5
( a 3 b )( a 2 b)( a 4 )
We are multiplying powers with the same base. Actually, we
have two bases (a and b). So, we keep the bases and we add the
exponents. The answer will be a 9 b 2
Now we're going to work with expressions that have
coefficients. Remember that coefficients are the
numbers in front of the variables. When multiplying powers with
the same base, we add the exponents. We also multiply the
coefficients.
Example 6
( 5x )( 2x 2 )
The coefficients are 5 and 2 so we multiply those. The
exponents of x are 1 and 2 so we add those to get the answer 12y
3
Example 7
( -3y 2 )( -4y )
The coefficients are -3 and -4 so we multiply those. The
exponents of y are 2 and 1 so we add those to get the answer 12
y 3
Example 8
( -2x 2 y 3 z 4)( -xz )
The coefficients are -2 and -1 so we multiply those. The
exponents of x are 2 and 1, the exponent of y is 3, and the
exponents of z are 4 and 1 so we add those to get the answer 2
x 3 y 3 z 5
Example 9
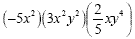
The coefficients are -5, 3, and 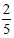 so we multiply those. The exponents of x are 2, 2,
and 1 and the exponents of y are 2 and 4 so we add those to get
the answer -6x 5 y 6
|
