Writing a Quadratic with Given Solutions
Not every quadratic equation can be solved by factoring, but the factoring method
can be used (in reverse) to write a quadratic equation with any given solutions. For
example, if the solutions to a quadratic equation are 5 and -3, we can reverse the
steps in the factoring method as follows:
| x = 5 |
or |
x |
= -3 |
|
| x - 5 = 0 |
or |
x + 3 |
= 0 |
|
| |
(x - 5)(x + 3) |
= 0 |
Zero factor property |
| |
x2 - 2x - 15 |
= 0 |
Multiply the factors. |
This method will produce the equation even if the solutions are irrational or
imaginary.
Example
Writing a quadratic given the solutions
Write a quadratic equation that has each given pair of solutions.
a) 4, -6
b)

c) -3i, 3i
Solution
a) Reverse the factoring method using solutions 4 and -6:
| x = 4 |
or |
x |
= -6 |
|
| x - 4 = 0 |
or |
x + 6 |
= 0 |
|
| |
(x - 4)(x + 6) |
= 0 |
Zero factor property |
| |
x2 + 2x - 24 |
= 0 |
Multiply the factors. |
b) Reverse the factoring method using solutions
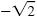 and and
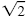 : :
x =
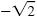
x +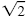 = 0
= 0 |
or or |
x x
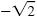 |
=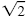
= 0 |
|
| |
(x +
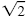 )(x )(x
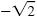 ) )
x2 - 2 |
= 0 = 0 |
Zero factor property Multiply the factors. |
c) Reverse the factoring method using solutions -3i and 3i:
| x = -3i x + 3i = 0 |
or or |
x x - 3i |
= 3i = 0 |
|
| |
(x + 3i)(x - 3i) x2
- 9i2
x2 + 9 |
= 0 = 0
= 0 |
Zero factor property Multiply the factors
Note: i2 = -1 |
|