Solving Quadratic Equations by Graphing
Objective Help you understand that the
solutions of a quadratic equation occur where the graph of the
corresponding function intersects the x-axis.
In this lesson, you should be able to use the graphing
techniques you already learned to help you solve or approximate
solutions to quadratic equations. Let's begin by stating a
definition.
Quadratic Equations
Quadratic Equation
A quadratic equation is an equation of the form f ( x ) = 0,
where f ( x ) = ax 2 + bx + c is a quadratic function.
The goal in solving a quadratic equation is to find what x
values make the y value of the quadratic function y = f ( x )
equal to zero. The y value of the function will be zero where the
graph intersects the x-axis. Geometrically, this is because a
solution of an equation f ( x ) = 0 occurs when the graph of the
function y = f ( x ) intersects the line y = 0. But the line y =
0 is the x-axis.
Recall that the graph of a quadratic function is a parabola.
So the solutions of a quadratic equation occur where the parabola
representing the graph of the quadratic intersects the x-axis.
Try to draw some parabolas like the following, and observe
that a parabola can either
• not intersect the x-axis,
• intersect the x -axis in exactly one point, or
• intersect the x -axis in two points.
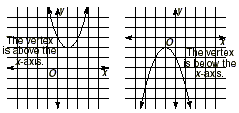
1. There may be no real solutions. This will
occur if the parabola does not intersect the x-axis. Either the
parabola opens upwards and the vertex (a minimum) lies above the
x -axis, or the parabola opens downwards and the vertex (a
maximum) lies below the x-axis.
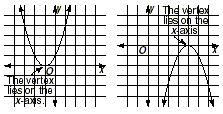
2. There may be one solution. This occurs
when the parabola intersects the x -axis in exactly one point.
This happens when the vertex of the parabola lies on the x -axis.
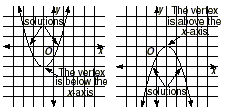
3. There may be two solutions. This occurs
when the parabola intersects the x -axis in two points. Either
the parabola opens upward and the vertex lies below the x -axis,
or the parabola opens downward and the vertex lies above the x
-axis.
Keep in mind that a quadratic equation may have no solutions,
one solution, or two solutions, because a parabola can intersect
the x -axis in zero, one, or two points.
|