Families of Functions
Functions that are related in some way are often called a family.
For example, linear functions that have the same slope form a family. The
graphs of these functions are parallel lines.
Let’s look at the graphs of the functions:
f(x) = -2x
f(x) = -2x - 3
f(x) = -2x + 4
Here are some points that satisfy each of these functions:
|
x |
f(x) = -2x |
f(x) = -2x - 3 |
f(x) = -2x + 4 |
|
-2 0
2 |
(-2, 4) (0, 0)
(2, -4) |
(-2, 1) (0, -3)
(2, -7) |
(-2, 8) (0, 4)
(2, 0) |
The graphs of the functions are shown. Notice the relationship between the
three graphs.
• The top graph is f(x) = -2x.
• The second graph is f(x) = -2x - 3. Notice that for each input x, the
output is 3 less than f(x) = -2x. This means that the graph of
f(x) = -2x - 3 is the same as that of f(x)The graph of f(x)
2
3
x is shown. Line A and Line B are parallel to f(x).
a. Find the equation of the function for Line A.x except that it is
shifted down 3 units.
• The third graph is f(x) = -2x + 4. Notice that for each input x, the
output is 4 more than f(x) = -2x. This means that the graph of
f(x) = -2x + 4 is the same as that of f(x) = -2x except that it is
shifted up 4 units.
This means that we could graph all three functions by first graphing
f(x) = -2x. Then, we could draw the graph of f(x) = -2x - 3 by shifting
the graph of f(x) = -2x down 3 units. Likewise, we could draw the graph
of f(x) = -2x + 4 by shifting the graph of f(x) = -2x up 4 units.
Example
The graph of
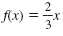 is shown. Line A and Line B are parallel to f(x).
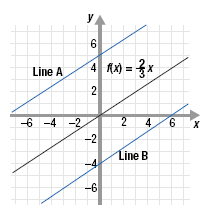
a. Find the equation of the function for Line A.
b. Find the equation of the function for Line B.
Solution
a. Line A is the function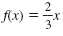
shifted up 5 units. So, the function for Line A is
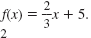
b. Line B is the function
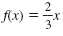shifted down 4 units. So, the function for Line B is
|
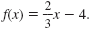
