Decimals and Fractions
0.6 ÷ 0.05 = ?
Lets start with something familiar that we can do (by long
division), namely
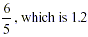
Then, examine the effect of the differences between what we
did (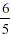 ) and what we should have done :
(a) Firstly, we divided a 6, but here we must divide something
10 times smaller (0.6), therefore the resulting answer will be 10
times smaller.
(b) Next, the effect of 5 instead of 0.05: we divided between
5 receivers, but now we must divide between fewer receivers, so
the resulting portions will, of course, be greater. How many
times greater?
We now use 0.05, which is 100 times smaller than the 5 we used
previously: i.e. we now divide the cake between 100 times fewer
'receivers' than previously, so the resulting portions will be
100 times larger.
Taking the effects of (a) and (b) together:
the 1.2 was made 10 times smaller, and then 100 times greater:
net effect: 10 times greater (than 1.2).
So, 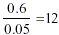 (We have obtained this result by using logic, not
rules).
Alternative method:
The problem arose from dividing by a fraction, 0.05. So,
remove this obstacle by replacing the fraction by a manageable 5.
This makes the divider 100 times greater. But we must not change
the result! So, dividing between 100 times more receivers, we
need 100 times more of what we are dividing (the 0.6), that is,
we need 100x0.6 which is 60.
So, the task of becomes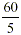 
, which, again, is 12.
|
