Roots and Powers
The Relationship Between Roots and Powers
Let’s look again at the relationship between taking a square root
and squaring.
| For example, let’s start with the number 6.
|
6 |
|
| Take its square root.
|
 |
|
| Square the square root.
|
 |
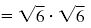 |
| Write the product as a single radical.
|
|
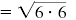 |
| Multiply.
|
|
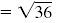 |
| Simplify.
|
|
= 6 |
| The result, 6, is the number that we started with. |
|
|
Thus, squaring “undoes†taking a square root.
Here, we saw that
 = 6.
= 6.
This is true in general.
Property —
Raising an nth Root to the nth Power
English Raising the nth root of a number to the nth power results in
the original number.
Algebra If
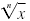 is defined, then is defined, then
 Here, n is a positive integer. Here, n is a positive integer.
Example
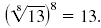
Example 1
Simplify:

Solution
Use this relationship to simplify each radical:
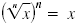

Note:
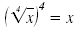 only when x
≥ 0. An even root
of a negative number is not a real number. only when x
≥ 0. An even root
of a negative number is not a real number.
Now, let’s see what happens when we first square a negative number, and
then take its square root.
| For example, let’s start with the number -4.
Square the number. The result is positive.
|
-4 (-4)2 |
= 16 |
| Take the square root.
|
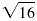 |
|
| Simplify. |
|
= 4 |
The result, 4, is the opposite of the number we started with.
Thus, when we square a negative number, and then take the square root,
we obtain the opposite of the original number.
This relationship holds true, in general for even roots.
|