Factoring Trinomials
After studying this lesson, you will be able to:
Steps of Factoring:
1. Factor out the GCF
2. Look at the number of terms:
- 2 Terms: Look for the Difference of 2 Squares
- 3 Terms: Factor the Trinomial
- 4 Terms: Factor by Grouping
3. Factor Completely
4. Check by Multiplying
This lesson will concentrate on the second step of factoring:
Factoring Trinomials.
**When there are 3 terms, we are factoring trinomials. Don't
forget to look for a GCF first.**
Factoring trinomials often requires some trial and error.
Don't get frustrated. Try all possible combinations. In the
previous problems, the first term has not had a coefficient. We
will now look at problems that do have coefficients in the first
term. This adds another level of trial and error or
"guessing".
One thing that will make the "guessing" more
accurate is to look for a prime number in the first term or the
constant term. Remember, a prime number only has 2 factors.....1
and itself. If the coefficient of the first term or the constant
term is prime, start there and "lock in" those factors.
Example 1
Factor 6x 2 - 13x - 5
This is a trinomial (has 3 terms). There is no GCF other than
one. So, we start with 2 parentheses:
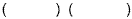
Using our signs rules, we can determine the signs for the
factors. The constant term is negative so we know the signs will
be different. Keep this in mind.
1 st : Since the coefficient of the constant term is prime
(5), we will start with the constant term. Find the factors of
the constant term. The factors of 5 are 1 and 5 . These go in the
last positions. We won't put the signs in yet because we aren't
sure where they go.
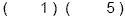
2 nd : Find the factors of the first term. The factors of 6x
2 are 1x, 6x and 2x, 3x. Remember, we need the
inside/outside combination to add up to the middle term which is
-13x. This time we don't just consider the factors of the
constant term because the first term also had factors. Here's
where the guessing comes in. Let's try the factors 2x,3x and see
what happens.
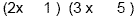 Notice we still didn't put in the signs. Let's check
the inside/outside combination. If we multiply inside, 1 times 3x
gives us 3x. Multiplying outside 2x times 5 gives us 10x. Now
remember, we have to have different signs. On the inside/outside
combination we have 3x and 10x. Using different signs, we cannot
make the combination equal the middle term. We resort to
guessing. Let's reverse the 2x and 3x and see what happens. Notice we still didn't put in the signs. Let's check
the inside/outside combination. If we multiply inside, 1 times 3x
gives us 3x. Multiplying outside 2x times 5 gives us 10x. Now
remember, we have to have different signs. On the inside/outside
combination we have 3x and 10x. Using different signs, we cannot
make the combination equal the middle term. We resort to
guessing. Let's reverse the 2x and 3x and see what happens.
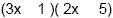 Notice we still didn't put in the signs. Let's check
the inside/outside combination. If we multiply inside, 1 times 2x
gives us 2x. Multiplying outside 3x times 5 gives us 15x. Now
remember, we have to have different signs. On the inside/outside
combination we have 2x and 15x. If we make the 15x negative and
the 2x positive we will have the combination of -13x...which is
our middle term. Notice we still didn't put in the signs. Let's check
the inside/outside combination. If we multiply inside, 1 times 2x
gives us 2x. Multiplying outside 3x times 5 gives us 15x. Now
remember, we have to have different signs. On the inside/outside
combination we have 2x and 15x. If we make the 15x negative and
the 2x positive we will have the combination of -13x...which is
our middle term.
(3x + 1 ) (2x - 5)
Check by using FOIL (3x + 1) (2x - 5) 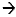 6x 2 - 15x + 2x - 5 which is
6x 2 - 13x - 5 6x 2 - 15x + 2x - 5 which is
6x 2 - 13x - 5
|