Powers of ten (Scientific Notation)
In so-called scientific notation , numbers are written as a
product of two parts:
(i) a number between 1 and 9.9999…..
and
(ii) a power of 10.
To convert a number to scientific notation, just move the
decimal point from its initial position until it is just to the
right of the first nonzero digit. The number of positions you
move the decimal point gives the numerical value of the power of
10 required. If the decimal point was moved to the left, the
power of 10 is positive. If the decimal point was moved to the
right, the power of 10 is negative.
Examples:

(Note that 4.3257 × 10 3 = 4.3257 × 1000 =
4325.7, demonstrating that the scientific notation form is the
same numerical value as the original number.)
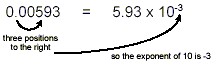
(Note that 5.93 × 10 -3 = 5.93 × 0.001 = 0.00593,
demonstrating that the scientific notation form is the same
numerical value as the original number.)
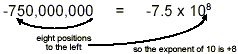
(Note that -7.5 × 10 8 = -7.5 × 100,000,000 =
-750,000,000, demonstrating that the scientific notation form is
the same numerical value as the original number.)
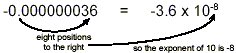
(Note that -3.6 × 10 -8 = -3.6 × 0.00000001 =
-0.000000036, demonstrating that the scientific notation form is
the same numerical value as the original number.)
Notice that the number itself can be positive or negative and
the exponent on the 10 can be positive or negative, and that
these two signs are quite independent of each other.
Obviously, to convert back from scientific notation to
ordinary decimal numbers, you just move the decimal point the
number of places left or right as indicated by the power of 10.
Examples:
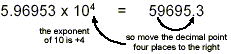
(Or, using ordinary arithmetic, 5.96953 × 10 4 =
5.96953 × 10,000 = 59695.3.)
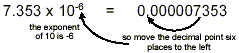
(Or, using ordinary arithmetic, 7.353 × 10 -6 =
7.353 × 0.000001 = 0.000007353.)
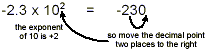
(Or, using ordinary arithmetic, -2.3 × 10 2 = -2.3 × 100 =
-230.)
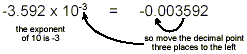
(Or, using ordinary arithmetic, -3.592 × 10 -3 = -3.592 ×
0.001 = -0.003592.)
To help you remember these rules, just keep in mind that when
the power of 10 is positive, the original numerical value was
bigger than 1. When the power of 10 is negative, the original
numerical value was a fraction, smaller than 1. The rules are not
something new or mysterious. As shown in brackets following each
example above, the rules just reflect simple numerical properties
– they produce the result of ordinary multiplication by
powers of 10.
If you have a scientific calculator capable of handling
scientific notation, then entry of such numbers is
straightforward. First key in the numerical part. Then press a
key (typically it has an upper case ‘E’ on it) and key
the exponent. You could use the above example as a test case for
checking to see that you know how to enter numbers in scientific
notation into your calculator.
Remark 1:
The use of scientific notation solves the problem of how to
distinguish between trailing zeros in whole numbers which are
significant, and those which are present only to tell us where
the decimal point is located (and so are not significant digits).
(To review the nature of this problem, just re-read the previous
document on significant digits.)
When we use scientific notation, there can be no trailing
zeros to the left of the decimal point. The only trailing zeros
in a number in scientific notation are to the right of the
decimal point, and therefore are automatically significant
digits, according to the rules.
So, for example
32000 is written 3.2 × 10 4 if none of the three
zeros are significant.
32000 is written 3.20 × 10 4 if just the first of
the three zeros is significant, but the remaining two zeros are
present only to locate the decimal point.
32000 is written 3.200 × 10 4 if just the first
two of the three zeros are significant, but the third zero is
present only to locate the decimal point. 32000 is written
3.2000 × 10 4 if all three zeros are significant.
|