Simplifying Rational Expressions
Objective Learn how to find excluded values
of a rational expression, and to simplify rational expressions.
Excluded Values
Definition of Rational Expression A rational
expression is an algebraic fraction whose numerator and
denominator are polynomials.
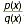 , where p(x) and q(x)
are polynomials
The term rational comes from the word ratio.
A rational expression can be described as a ratio of polynomials.
A rational function is also a ratio of
polynomials, as shown below.
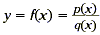
Notice that f ( x ) cannot be defined for values of x when the
denominator q ( x ) equals 0, since division by 0 is undefined.
So these values are excluded from the domain of f ( x ).
Example 1
Find the excluded values of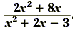 
Solution
The excluded values are those values of x where the
denominator x 2 + 2x - 3 equals 0. Since these are the
roots of the denominator, solve x 2 + 2x - 3 = 0.
The easiest way to solve this quadratic equation is by
factoring and then using the Zero Product Property.
| x 2 + 2x - 3 = 0 |
|
| (x - 1)(x + 3) = 0 |
Factor. |
| x - 1 = 0 or x + 3 = 0 |
Zero Product Property |
| x = 1 or x = -3 |
|
So, the excluded values are x = 1 and x = - 3. Said another
way, the domain of the rational function 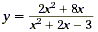 consists of all values
of x except x = 1 and x = -3.
Example 2
Find the excluded values of  .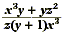
Solution
The excluded values are the zeros of denominator, z( y + 1)x
3 . Use the Zero Product Property to find these values.
z( y + 1)x 3 = 0
z = 0 or y + 1 + 0 or x 3 = 0
y = -1, or x = 0
So, the excluded values are z = 0, y = -1, and x = 0.
Simplifying Rational Expressions
Remember that to simplify a rational number such as 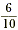 , you should look for
the greatest common factor (GCF) of the numerator and the
denominator, and cancel this common factor.
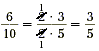
Simplifying rational expressions can be done the same way.
Factor the numerator and the denominator, and cancel the greatest
common factor.
Example 3
Simplify  .
Solution
First, find the GCF of the numerator and the denominator. The
numerator x + 2 is completely factored. Factor the denominator.
x 2 - 4 = ( x - 2)( x + 2)
So, the GCF of the numerator and the denominator is x + 2. Now
simplify the expression by canceling this GCF.
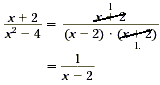
Example 4
Simplify  .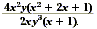
Solution
First, find the GCF of the numerator and the denominator.
Notice that the denominator 2xy 3( x + 1) is
completely factored. However, the numerator can be factored
further.
4x 2y( x 3 + 2 x + 1) = 2 · 2x 3y(
x + 1) 3
Comparing the factors of the numerator and the denominator, we
see that the greatest common factor of the numerator and
denominator is
2xy( x + 1).
Therefore, simplify the expression by canceling this GCF.
|
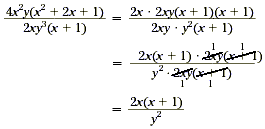
