Percent of Change
Objective Learn how to find the percent of
change of a certain quantity.
When a certain quantity varies, it is usually important to
know by what percent it changed. Here you will learn how to find
the percent of change. Start with the following example.
Finding Percent of Change
Example 1
Find the percent of change from 160 to 180.
Solution
There are two possible ways to solve this problem.
Method 1
First, find the amount of change. Then compare the amount of
change to the original amount. The amount of change is 180 - 160
or 20. That is, the quantity increased by 20. Now, compare the
amount of change to the original amount. Let x represent the
percent of change. The following equation results.
| 20 |
= x% × 160 |
|
| 20 |
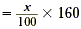 |
Rewrite x% as 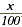 |
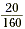 |
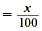 |
Divide each side by 160. |
| 2000 |
= 160x |
Find the cross products. |
| 12.5 |
= x |
|
So, the percent change from 160 to 180 is 12.5%.
Method 2
To find the percent of change from 160 to 180 essentially
means to find
What percent is 180 of 160?
Let y represent this percent. The following equation results.
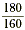 |
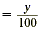 |
|
| 18,000 |
= 160y |
Write the cross products. |
| 112.5 |
= y |
|
This means that 180 is 112.5% of 160. Since 100% of a number
is equal to that number, the percent of increase is 112.5% - 100%
or 12.5%.
A shortcut to Method 2 is to divide the new amount by the
original amount, subtract 1, and then express the decimal as a
percent.
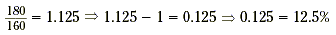
|