Logarithmic Functions
Recall that all exponential functions of the form y = bx where a > 0 and a
≠ 1 are one-to-one. This means that they have inverses. Their inverses satisfy the equation: x
= by (b > 0, b ≠ 1)
These inverse functions, when solved for y, are called Logarithmic Functions.
The , where b > 0, b ≠ 1, is denoted by y
= log b x and is defined by:
y = log b x iff x = by
In words, this definition says: "y is the power (exponent) to which b must be raised in order to get x".
What you need to remember is that a logarithm is an exponent.
In the above definition, y is the logarithm and y is the exponent.
Examples:
| 1) 25 = 32 |
is equivalent to |
5 = log 2 32 |
| 2) 102 = 100 |
is equivalent to |
2 = log 10 100 |
3)
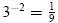 |
is equivalent to |
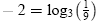 |
| 4) 61 = 6 |
is equivalent to |
1 = log 6 6 |
| 5) 70 = 1 |
is equivalent to |
0 = log 7 1 |
To find the exact value of a logarithm, we write the logarithm in exponential notation and use this property
of exponential functions:
ONE-TO-ONE PROPERTY OF EXPONENTS:
If au = av, then u = v
Domain of a Logarithmic Function
Remember that an exponential function has domain, D = the set of real numbers and range, R
= the set of positive real numbers. Therefore, since they are inverses, the domain
of a logarithmic function must be D = the set of positive real numbers, and its range must be R
= the set of real numbers.
This means that the argument of a logarithm must always be positive ( greater than 0).
Graphs of Logarithmic Functions
The functions y = bx and y = log b x are inverses of each other. Recall what the graph of y
= bx looks like. Then try to picture the graph of its reflection through the line y
= x.
All graphs of the form y = log b x, when b > 1, will have the same basic shape as this one.
Facts About the Graphs of Logarithmic Functions f(x) = log b x
1) The domain is the set of positive real numbers; the range is all real numbers.
2) The x-intercept is 1; there is no y-intercept.
3) The y-axis (x = 0) is the vertical asymptote.
4) f(x) = log b x, b >1, is an increasing function and is one-to-one.
f(x) = log b x, 0 < b < 1, is a decreasing function and is one-to-one.
5) The graph contains the points (1, 0) and (b, 1).
6) The graph is smooth and continuous with no corners or gaps.
COMMON LOGARITHMS are logarithms with base 10. The common logarithmic function would be
y = log 10 x, except that the 10 is not written.
y = log x ↔ 10y = x
In words, "y is the exponent to which 10 must be raised in order to get x".
log 100 = 2, since 102 = 100
log 1000 = 3, since 103 = 1000
log (0.1) = -1, since 10-1 = 0.1
The Natural Logarithmic Function
Recall y = ex, the exponential function. Its inverse would be a logarithmic function with base e, or
y = log e x. However, because of the significance of the number e, this logarithmic function has a special oe e
name, the natural logarithmic function, and it is written ln x.
Definition of The Natural Logarithmic Function:
y = ln x iff x = ey
In words: "y is the exponent to which e must be raised in order to get x".
Since e is a number greater than 1, the graph of the natural logarithmic function is shaped like the graph of
y = log 2 x:
If we need to find logarithmic values in bases other than 10 and e, we can use a formula called the:
CHANGE-OF-BASE FORMULA: If b > 0, b ≠ 1, c
> 0, c ≠ 1and x > 0, then
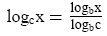
|