Finding Factors
Examples with Solutions
EXAMPLE 1
What are the factors of 45?
Solution
Let’s see if 45 is divisible by 1, 2, 3, and so on, using
the divisibility tests wherever they apply.
| Is 45 divisible by
|
Answer
|
| 1? |
Yes, because 1 is a factor of any number;
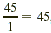 , so 45 is also a factor. |
| 2? |
No, because the ones digit is not even. |
| 3? |
Yes, because the sum of the digits, 4 + 5
= 9, is divisible by 3; 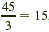 , so 15 is also a factor. |
| 4? |
No, because 4 will not divide into 45
evenly. |
| 5? |
Yes, because the ones digit is 5; 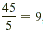 , so 9 is also a factor. |
| 6? |
No, because 45 is not even. |
| 7? |
No, because 45 ÷ 7 has remainder 3. |
| 8? |
No, because 45 ÷ 8 has remainder 5. |
| 9? |
We already know that 9 is a factor. |
The factors of 45 are therefore 1, 3, 5, 9, 15, and 45.
Note that we really didn’t have to check to see if 9 was
a factor—we learned that itwas when we checked for
divisibility by 5. Also, because the factors were beginning
torepeat with 9, there was no need to check numbers greater than
9.
EXAMPLE 2
Identify all the factors of 60.
Solution
Let’s check to see if 60 is divisible by 1, 2, 3, 4, and
so on.
| Is 60 divisible by
|
Answer
|
| 1? |
Yes, because 1 is a factor of all
numbers; 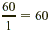 , so 60 is also a factor. |
| 2? |
Yes, because the ones digit is even; 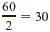 , so 30 is also a factor. |
| 3? |
Yes, because the sum of the digits, 6 + 0
= 6, is divisible by 3;  , so 20 is also a factor. |
| 4? |
Yes, because 4 will divide into 60
evenly; 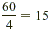 , so 15 is also a factor. |
| 5? |
Yes, because the ones digit is 0; 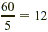 , so 12 is also a factor. |
| 6? |
Yes, because the ones digit is even and
the sum of the digits is divisibleby 3; 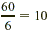 , so 10 is also a factor. |
| 7? |
No, because 60 ÷ 7 has remainder 4. |
| 8? |
No, because 60 ÷ 8 has remainder 4. |
| 9? |
No, because the sum of the digits, 6 + 0
= 6, is not divisible by 9. |
| 10? |
We already know that 10 is a factor. |
The factors of 60 are therefore 1, 2, 3, 4, 5, 6, 10, 12, 15,
20, 30, and 60. Can you explain how we knew that 10 was a factor
of 60 when we checked for divisibility by 6?
EXAMPLE 3
A presidential election takes place in the United States every
year thatis a multiple of 4. Was there a presidential election in
1866?
Solution
The question is: Does 4 divide into 1866 evenly? Using the
divisibility test for 4, we check whether 66 is a multiple of 4.
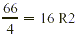
Because 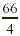 has remainder 2, 4 is not a factor of 1866. So there
was nopresidential election in 1866.
|
